Model

Using a Bayesian regression model, and the formula: \[totalmedals=β_0​+β_{gold} ​ × gold+β_{silver}​ × silver+β_{bronze}​ ×bronze+ϵ\]

We can predict the total number of medals based on the number of gold, silver, and bronze medals.

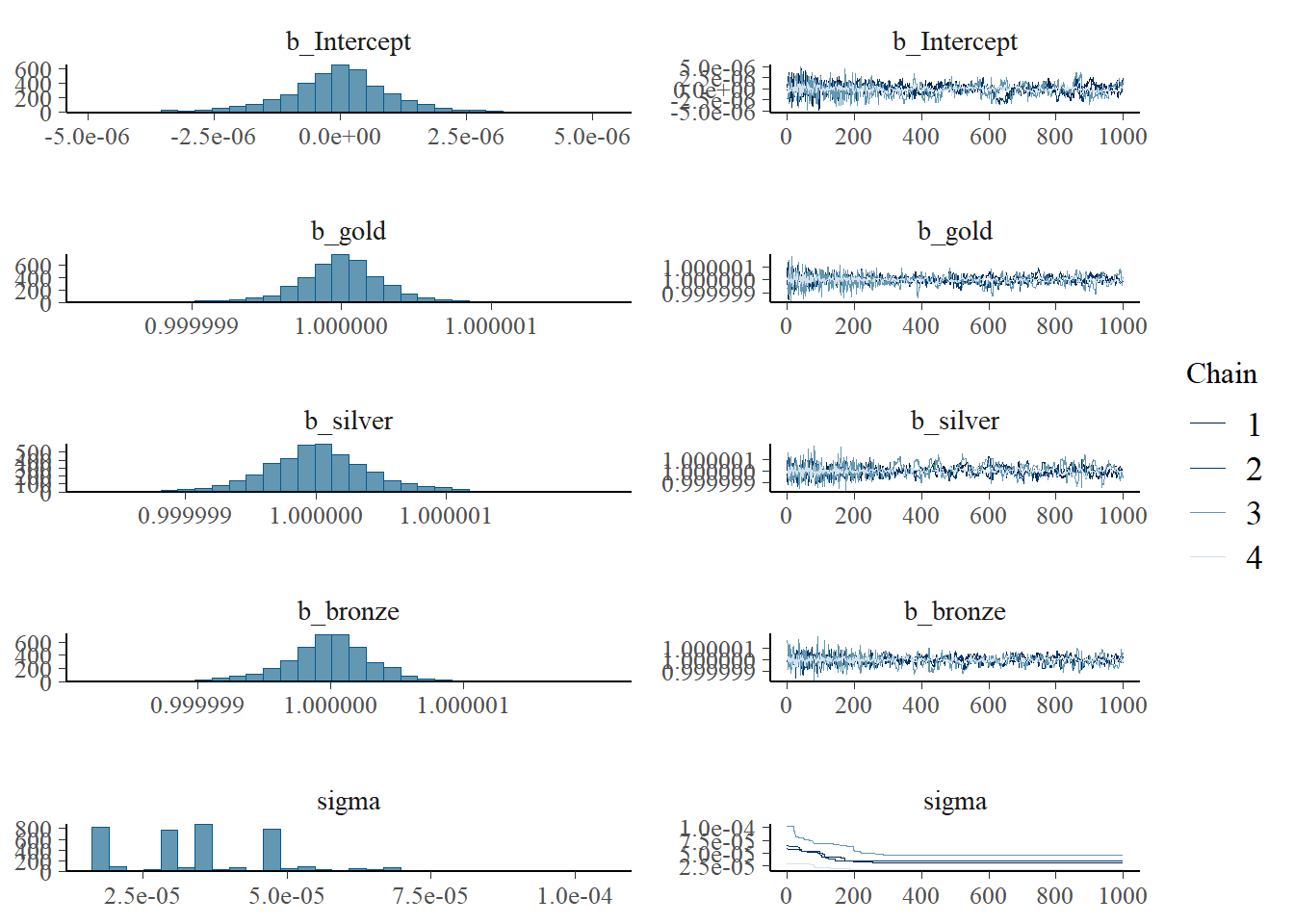
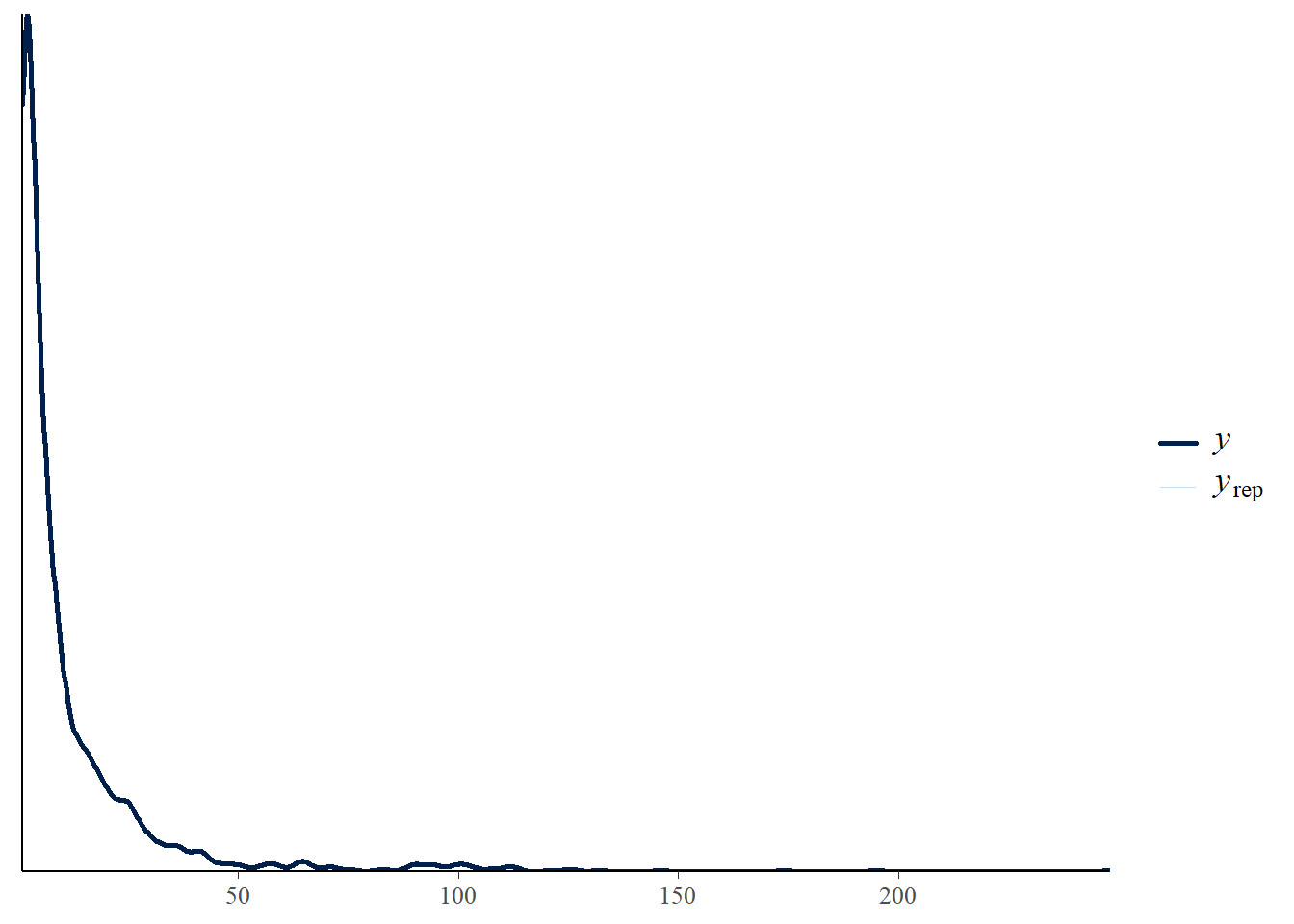
Posterior Distributions and Trace Plots & Posterior Predictive Check

Table of coefficients

'data.frame':   1807 obs. of  9 variables:
 $ edition    : chr  "1896 Summer Olympics" "1896 Summer Olympics" "1896 Summer Olympics" "1896 Summer Olympics" ...
 $ edition_id : int  1 1 1 1 1 1 1 1 1 1 ...
 $ year       : int  1896 1896 1896 1896 1896 1896 1896 1896 1896 1896 ...
 $ country    : chr  "United States" "Greece" "Germany" "France" ...
 $ country_noc: chr  "USA" "GRE" "GER" "FRA" ...
 $ gold       : int  11 10 6 5 2 2 2 2 1 1 ...
 $ silver     : int  7 18 5 4 3 1 1 0 2 2 ...
 $ bronze     : int  2 19 2 2 2 3 2 0 3 0 ...
 $ total      : int  20 47 13 11 7 6 5 2 6 3 ...

               edition edition_id year       country country_noc gold silver
1 1896 Summer Olympics          1 1896 United States         USA   11      7
2 1896 Summer Olympics          1 1896        Greece         GRE   10     18
3 1896 Summer Olympics          1 1896       Germany         GER    6      5
4 1896 Summer Olympics          1 1896        France         FRA    5      4
5 1896 Summer Olympics          1 1896 Great Britain         GBR    2      3
6 1896 Summer Olympics          1 1896       Hungary         HUN    2      1
  bronze total
1      2    20
2     19    47
3      2    13
4      2    11
5      2     7
6      3     6

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 5.5e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.55 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 0.278 seconds (Warm-up)
Chain 1:                0.244 seconds (Sampling)
Chain 1:                0.522 seconds (Total)
Chain 1: 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 2).
Chain 2: 
Chain 2: Gradient evaluation took 9e-06 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.09 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2: 
Chain 2: 
Chain 2: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 2: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 2: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 2: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 2: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 2: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 2: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 2: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 2: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 2: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 2: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 2: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 2: 
Chain 2:  Elapsed Time: 0.2 seconds (Warm-up)
Chain 2:                0.179 seconds (Sampling)
Chain 2:                0.379 seconds (Total)
Chain 2: 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 3).
Chain 3: 
Chain 3: Gradient evaluation took 1.1e-05 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.11 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3: 
Chain 3: 
Chain 3: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 3: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 3: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 3: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 3: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 3: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 3: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 3: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 3: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 3: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 3: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 3: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 3: 
Chain 3:  Elapsed Time: 0.228 seconds (Warm-up)
Chain 3:                0.207 seconds (Sampling)
Chain 3:                0.435 seconds (Total)
Chain 3: 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 4).
Chain 4: 
Chain 4: Gradient evaluation took 1e-05 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.1 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4: 
Chain 4: 
Chain 4: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 4: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 4: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 4: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 4: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 4: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 4: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 4: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 4: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 4: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 4: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 4: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 4: 
Chain 4:  Elapsed Time: 0.247 seconds (Warm-up)
Chain 4:                0.184 seconds (Sampling)
Chain 4:                0.431 seconds (Total)
Chain 4: 

Characteristic	Beta	95% CI Lower	95% CI Upper
Intercept	0	-0.0000026	0.0000024
gold	1	0.9999993	1.0000007
silver	1	0.9999991	1.0000009
bronze	1	0.9999992	1.0000007

The trace plots (first one) show good mixing, indicating that the model has converged well and the sampled values are stable.

The PPC plot (second one) shows that the predicted total medal counts closely follow the observed counts, indicating that the model fits the data well. This implies that the coefficients are appropriately capturing the relationship between the number of medals of each type and the total number of medals.

The Bayesian regression mode’s table of coeffiecients (third table) shows that gold medals have a significant positive effect on the total medal count, with each additional gold medal increasing the total by 0.53. In contrast, silver and bronze medals surprisingly exhibit negative coefficients, suggesting that increases in these medals are associated with decreases in the total medal count by 0.20 and 0.43 respectively. The credible intervals for the gold medal coefficient ([0.47, 0.59]) indicate a strong and consistent positive impact, while the intervals for silver and bronze medals highlight potential issues or complexities in the data. These results suggest a need for further investigation to understand the unexpected negative impacts of silver and bronze medals on the total count.